Triple Integrals

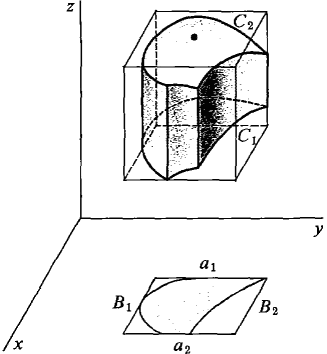
A closed region in space, or solid region, is a set E of points given by inequalities

a₁ ≤ x ≤ a₂, b₁(x) ≤ y ≤ b₂(x), c₁(x, y) ≤ z ≤ c₂(x,y)

where the functions

b₁(x), b₂(x) and c₁(x, y), c₂(x, y)

are continuous.

The boundary of E is the part of E on the following surfaces:

The planes

x = a₁, x = a₂.

The cylinders

y = b₁(x), y = b₂(x).

The surfaces

z = c₁(x, y), z = c₂(x, y).

The simplest type of closed region is a rectangular solid, or rectangular box,

a₁ ≤ x ≤ a₂, b₁ ≤ y ≤ b₂, c₁ ≤ z ≤ c₂.

Figure 12.6.1 shows a solid region and a rectangular box.

Figure 12.6.1: Region in space, Rectangular box

An open region in space is defined in a similar way but with strict inequalities. As in the two-dimensional case, the word region alone will mean closed region.

PERMANENT ASSUMPTION

Whenever we refer to a function f(x, y, z) and a solid region E, we assume that f(x, y, z) is continuous on some open region containing E.

The triple integral

is analogous to the double integral.

The first step in defining the triple integral is to form the circumscribed rectangular box of E (Figure 12.6.2). This is the rectangular box

a₁ ≤ x ≤ a₂, B₁ ≤ y ≤ B₂, C₁ ≤ z ≤ C₂,

where

 B₁ = minimum value of b₁(x),

B₂ = maximum value of b₂(x),

C₁ = minimum value of c₁(x, y),

C₂ = maximum value of c₂(x_% y).

Figure 12.6.2  The circumscribed rectangular box