| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Double Integrals in Polar Coordinates Double Integrals in Polar Coordinates  Problems Problems |
|






|
|
Problems
In Problems 1-16, find the volume using polar coordinates.
17 Find the volume of the solid over the cardioid r = 1 + cos θ between the plane z = 0 and the cone z = r. 18 Find the volume of the solid over the cardioid r = 1 + cos θ between the paraboloids z = r2 and z = 8 - r2. 19 Find the volume of the solid over the circle r = sin θ between the plane z = 0 and the hemisphere 20 Find the volume of the solid over the circle r = 2 cos θ between the plane z = 0 and the cone z - 1 - r. 21 Find the volume of the solid over the polar rectangle α ≤ θ ≤ β, a ≤ r ≤ b, between the plane z = 0 and the cone z = r. 22 Find the volume of the portion of the hemisphere 23 A circular object of radius b has density equal to the distance from the outside of the circle. Find (a) the mass, (b) the moment of inertia about the origin. 24 A circular object of radius b has density equal to the cube of the distance from the center. Find (a) the mass, (b) the moment of inertia about the origin. 25 Find the moment of inertia about the origin of a circular ring a ≤ r ≤ b, 0 ≤ θ ≤ 2n, of constant density k. 26 Find the moment of inertia of a circular object of radius b and constant density k about a point on its circumference. (The center can be put at (0, b), so the object is on the polar region 0 ≤ r ≤ 2b sin θ, 0 ≤ θ ≤ π.) 27 An object has constant density k on the circular sector 0≤x≤l,0≤y≤ 28 An object of constant density k covers the cardioid r ≤ 1 + cos θ, 0 ≤ θ ≤ 2π. Find (a) the center of mass, (b) the moment of inertia about the origin. 29 An object of constant density k covers the region inside the circle r = 2b sin θ and outside the circle r = b. Find (a) the center of mass, (b) the moment of inertia about the origin. 30 An object of constant density k covers the polar region 0 ≤ θ ≤ π/2, 0≤r≤b sin 2θ. Find (a) the center of mass, (b) the moment of inertia about the origin. 31
|
|
Home  Multiple Integrals Multiple Integrals  Double Integrals in Polar Coordinates Double Integrals in Polar Coordinates  Problems Problems |
|
Last Update: 2006-11-25



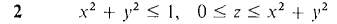








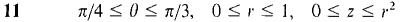


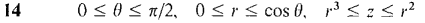



 over the polar rectangle α ≤ θ ≤ β, a ≤ r ≤ b (assuming b ≤ 1).
over the polar rectangle α ≤ θ ≤ β, a ≤ r ≤ b (assuming b ≤ 1). Find (a) the center of mass, (b) the moment of inertia about the origin.
Find (a) the center of mass, (b) the moment of inertia about the origin.