| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Triple Integrals Triple Integrals  Triple Riemann Sums Triple Riemann Sums |
|






|
|
Triple Riemann Sums
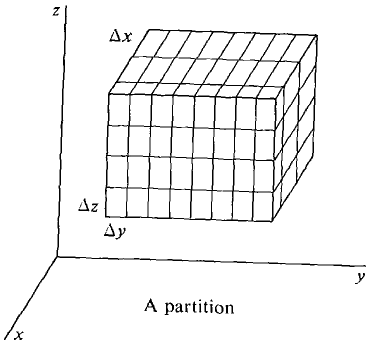
Our next step is to define the triple Riemann sum. Given positive real numbers Δx, Δy, and Δz, we partition the circumscribed rectangular box of E into rectangular boxes with sides Δx, Δy, and Δz (Figure 12.6.3). The partition points of this three-dimensional partition have the form (xk,yl,zm) 0 ≤ k ≤ n, 0 ≤ l ≤p, 0 ≤ m ≤ q. The triple Riemann sum of f(x, y, z) Δx Δy Δz over E is defined as the sum
When we replace Δx, Δy, Δz by positive infinitesimals dx, dy, dz we obtain an infinite triple Riemann sum
Figure 12.6.3 LEMMA For all positive infinitesimals dx, dy, and dz, the triple Riemann sum
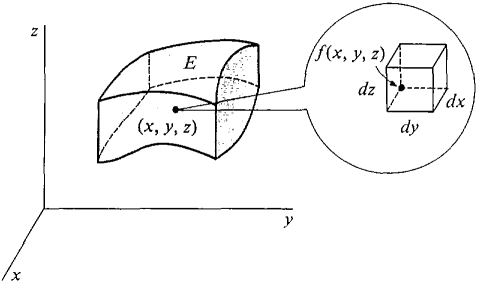
is a finite hyperreal number and therefore has a standard part. We are now ready to define the triple integral (see Figure 12.6.4).
Figure 12.6.4 DEFINITION Given positive infinitesimal dx, dy, and dz, the triple integral of a continuous function f(x, y, z) over E is
We shall now briefly state some basic theorems on triple integrals, which are exactly like the corresponding theorems for double integrals. INDEPENDENCE OF dx, dy, AND dz
ADDITION PROPERTY
|
|
Home  Multiple Integrals Multiple Integrals  Triple Integrals Triple Integrals  Triple Riemann Sums Triple Riemann Sums |
|
Last Update: 2010-11-25




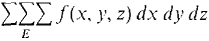
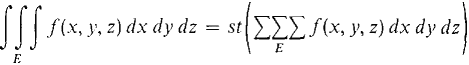
 does not depend on dx, dy, or dz.
does not depend on dx, dy, or dz. for
for
