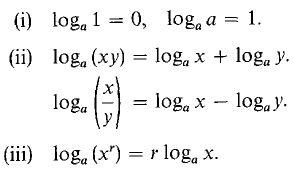Rules for Logarithms

The rules for exponents can be turned around to give rules for logarithms.

RULES FOR LOGARITHMS

Let a, x, and y be positive real numbers, a ≠ 1.

These rules are useful because they reduce multiplication to addition and exponentiation to multiplication.

Let us make a quick check to see that these rules are correct for logarithms to the base 10. Here is a short table of common logarithms.

To find common logarithms of larger or smaller numbers we can use the rule

log₁₀ 10ⁿy = n + log₁₀ y.

We try a few cases to see if the answers agree, to one decimal place. We write log x for log₁₀ x below.

We could do the same thing with any other base. Base 10 is convenient because a number in decimal notation immediately can be put in the form y = 10ⁿ z where 1 ≤ z ≤ 10.

The slide rule was a device for quickly looking up and adding logarithms. Slide rules were widely used before the advent of electronic calculators and give an interesting illustration of the rules of logarithms. If two ordinary rulers are slid together in slide rule fashion they can be used to compute the sum of two numbers, as shown in Figure 8.2.2.

Figure 8.2.2

In a slide rule, instead of marking off the distances 0, 1, 2, ..., 10, we mark off the distances

0 = log 1, log 2, log 3, ... log 10.

The marks will be unevenly spaced, being closer together toward the right. We can then use the slide rule to compute the sum of two logarithms, and therefore the product of two numbers, as shown in Figure 8.2.3.

Figure 8.2.3

We know all the numbers are logarithms, so we can make a less cluttered slide rule by removing all the "log" symbols, as in Figure 8.2.4.

Figure 8.2.4