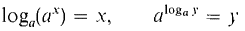| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Exponential and Logartihmic Functions Logarithmic Functions Logarithmic Functions - Definition |
|
 Search the VIAS Library | Index
|
  |
Logarithmic Functions - Definition
The inverses of exponential functions are called logarithmic functions. Inverse functions were studied in Sections 2.4 and 7.3. Given a positive real number a different from one, the exponential function with base a is either increasing or decreasing. Therefore it has an inverse function. DEFINITION Let a ≠ 1 be a positive real number. The logarithmic function with base a, denoted by x = logay, is defined as the inverse of the exponential function with base a, y = ax. That is, logay is defined as the exponent to which a must be raised to get y, logay = x if and only if y = ax. We see at once that
whenever loga y is defined. The logarithm of y to the base 10, written log y = log10 y, is called the common logarithm of y. Common logarithms are readily available in tables. Logarithmic functions underlie such aids to computation as the slide rule and tables of logarithms. Some of the most basic integrals, such as the integrals of 1/x and tan x, are functions that involve logarithms. THEOREM 1 If 0 < a and a ≠ 1, the function x = loga y is defined and continuous for y in the interval (0, ∞). We skip the proof, loga y is left undefined when either a ≤ 0, a = 1, or y ≤ 0. THEOREM 2 The function x = loga y is increasing if a > 1 and decreasing if a < 1. PROOF Case 1 a > 1. Let 0 < b < c. Then
We cannot have loga b ≥ loga c because the inequality (v) for exponents would then give b ≥ c. We conclude that loga b < loga c. Case 2 a < 1 is similar. In Figure 8.2.1 we have graphs of y = ax for a > 1 and for a < 1, and graphs of the inverse functions x = loga y.
Figure 8.2.1
|
|
| Home Exponential and Logartihmic Functions Logarithmic Functions Logarithmic Functions - Definition |
|
Last Update: 2006-11-25