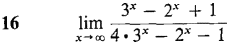| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Exponential Functions Exponential Functions  Problems Problems |
|






|
|
Problems
In Problems 1-7, verify the inequalities.
In Problems 8-23 evaluate the limit.
24 Prove that the function y = xx, x ≥ 1, is increasing. 25 Prove that if a > 0 and limx→c f(x) = L, then limx→c af(x) = aL. 26 Prove that for each real number r, the function y = xr, x > 0, is continuous.
|
|
Home  Exponential and Logartihmic Functions Exponential and Logartihmic Functions  Exponential Functions Exponential Functions  Problems Problems |
|
Last Update: 2006-11-25