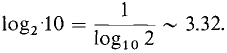The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Exponential and Logartihmic Functions Logarithmic Functions Rules For Changing Bases Of Logarithms
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Rules For Changing Bases Of Logarithms

There is a simple relationship between logarithms with two different bases.

RULES FOR CHANGING BASES OF LOGARITHMS

Let a, b, and y be positive and a,b ≠ 1. Then

08_exp-log_functions-44.gif

PROOF

a]°sab = b, so

08_exp-log_functions-45.gif

whence 08_exp-log_functions-46.gif

Setting a = y we get the equation logb a = 1/(loga b). If we hold the bases a and b fixed and let y vary, then the rule shows that loga y and logb y are proportional to each other, with the constant ratio

08_exp-log_functions-47.gif

Therefore a slide rule based on logarithms to the base 2, for example, would look exactly like a slide rule based on logarithms to the base 10 (common logarithms). If the same unit of length is used, all the distances would be multiplied by the constant factor

08_exp-log_functions-48.gif

So the slide rule would be similar but more than 3 times as big. Table 8.2.1 shows various logarithms with different bases.

Table 8.2.1

X 1

2

4

8

16

1

2

1 4

08_exp-log_functions-49.gif

log2 x 0

1

2

3

4

-1

-2

½

-3/2

log4 x 0

½

1

1½

2

-½

-1

¼

- ¾

log1/2 x 0

-1

-2

-3

-4

1

2

-½

3/2

log√a x 0

2

4

6

8

-2

-4

1

-3

Notice that for all x > 0,

08_exp-log_functions-50.gif

Also, for each base a, loga (1/x) = -loga x.

08_exp-log_functions-51.gif

Home Exponential and Logartihmic Functions Logarithmic Functions Rules For Changing Bases Of Logarithms

Last Update: 2006-11-08