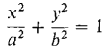The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Limits, Analytic Geometry, and Approximations Ellipses and Hyperbolas Sketching Hyperbolas and Summary
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Sketching Hyperbolas and Summary

Here are the steps for graphing a hyperbola y2/b2 - x2/a2 = 1.

GRAPHING A HYPERBOLA

05_limits_g_approx-322.gif

Step 1

Compute the values of a and b from the equation. Draw the rectangle with sides x = ±a, y = ±b.

Step 2

Draw the diagonals of the rectangle. They will be the asymptotes.

Step 3

Mark the vertices of the hyperbola at the points (0, ±b).

Step 4

Draw the upper and lower branches of the hyperbola, The upper branch has a minimum at the vertex (0, b), is concave upward, and approaches the diagonal asymptotes from above. The lower branch is a mirror image. See Figure 5.5.7.

05_limits_g_approx-325.gif

Figure 5.5.7

A hyperbola of the form

05_limits_g_approx-323.gif

is graphed in a similar manner, but with the roles of x and y reversed. There is a left branch and a right branch, which are vertical at the vertices (±a, 0).

Example 3

Using the method of this section, we can sketch the graph of any equation of the form

Ax2 + Cy2 + F = 0.

In the ordinary case where A, C, and F are all different from zero, rewrite the equation as

A1x2 + C1y = 1,

where A1 = -A/F, C1 = -C/F. There are four cases depending on the signs of A1 and C1, which are listed in Table 5.5.1.

Table 5.5.1

A1

C1

Graph of A1x2 + C1y2 = 1

>0

>0

ellipse05_limits_g_approx-327.gif

>0

<0

hyperbola05_limits_g_approx-328.gif

<0

>0

hyperbola05_limits_g_approx-329.gif

<0

<0

empty

If one or two of A, C, and F are zero, the graph will be degenerate (two lines, one line, a point, or empty).
Home Limits, Analytic Geometry, and Approximations Ellipses and Hyperbolas Sketching Hyperbolas and Summary

Last Update: 2006-11-05