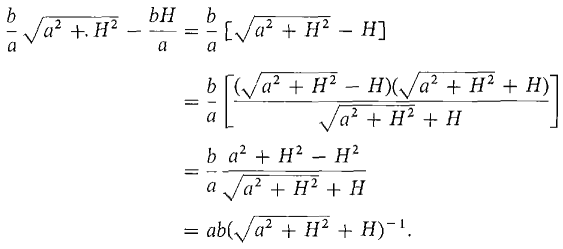Hyperbolas: Branches and Limits

Using derivatives and limits, we can get additional information that is helpful in sketching the graph of a hyperbola. By solving the equation

for y as a function of x, we see that the upper and lower branches have the equations upper branch:

lower branch:

We concentrate on the upper branch. Its first two derivatives, after some algebraic simplification, come out to be

Thus the first derivative is zero only at x = 0 (the vertex), and the second derivative is always positive. We have the following table of values for the upper branch.

All the limit computations are easy except for dy/dx, which we work out for x → ∞. Let H be positive infinite.

We carry out a similar computation for the limit as x →-∞. Let H be positive infinite.

The table shows that the upper branch is almost a straight line with slope -b/a for large negative x and almost a straight line with slope b/a for large positive x. In fact, we shall show now that the lines

y = bx/a, y = -bx/a

are asymptotes of the hyperbola. That is, as x approaches ∞ or -∞, the distance between the line and the hyperbola approaches zero. We show that the upper branch approaches the line y = bx/a as x→∞; that is,

Let H be positive infinite. Then

This is infinitesimal, so the limit is zero.