Example 6:

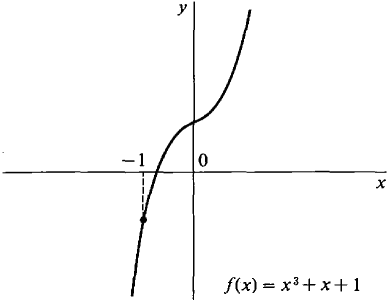
How many zeros does the function f(x) = x³ + x + 1 have? We use both Rolle's Theorem and the Intermediate Value Theorem.

Using Rolle's Theorem: f'(x) = 3x² + 1. For all x, x² ≥ 0, and hence f'(x) ≥ 1. Therefore f(x) has at most one zero.

Using the Intermediate Value Theorem: We have f(-1) = -1, f(0) = 1. Therefore f has at least one zero between -1 and 0.

CONCLUSION

f has exactly one zero, and it lies between -1 and 0 (see Figure 3.8.16).

Figure 3.8.16