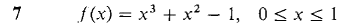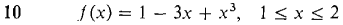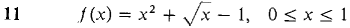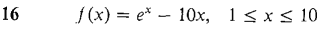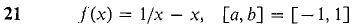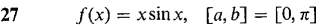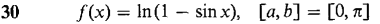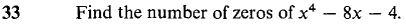Problems

In Problems 1-16, use the Intermediate Value Theorem to show that the function has at least one zero in the given interval.

In Problems 17-30, determine whether or not f' has a zero in the interval (a, b). Warning: Rolle's Theorem may give a wrong answer unless all the hypotheses are met.

In Problems 35-42, find a point c in (a, b) such that f(b) - f(a) = f'(c)(b - a).

43           Use Rolle's Theorem to show that the function f(x) = x³ - 3x + b cannot have more than one zero in the interval [-1, 1], regardless of the value of the constant b.

44           Suppose f, f', and f" are all continuous on the interval [a, b], and suppose f has at least three distinct zeros in [a, b] Use Rolle's Theorem to show that f" has at least one zero in [a, b]

45           Suppose that f"(x) > 0 for all real numbers x, so that the curve y = f(x) is concave upward on the whole real line as illustrated in the figure. Let L be the tangent line to the curve at x = c. Prove that the line L lies below the curve at every point x ≠ c.