Example 5:

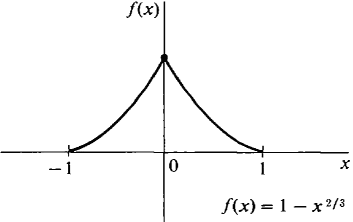
f(x) = 1 - x^2/3, a = -1, b = 1. Then f(-1) = f(1) = 0, and f'(x) = -⅔x^-1/3 for x ≠ 0. f'(0) is undefined. There is no point c in (-1, 1) at which f'(c) = 0. Rolle's Theorem does not apply in this case because f'(x) does not exist at one of the points of the interval (-1, 1), namely at x = 0. In Figure 3.8.15, we see that instead of being horizontal at a point in the interval, the curve has a sharp peak.

Figure 3.8.15

Rolle's Theorem is useful in finding the number of zeros of a differentiable function f. It shows that between any two zeros of f there must be one or more zeros of f'. It follows that if f' has no zeros in an interval I, then f cannot have more than one zero in I.