| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Continuous Functions Continuous Functions  Properties of Continuous Functions Properties of Continuous Functions  Examples Examples  Example 4 Example 4 |
|






|
|
Example 4

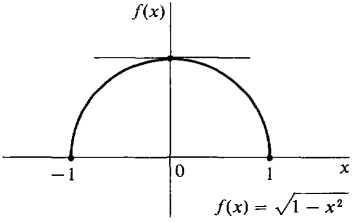
Figure 3.8.14
|
|
Home  Continuous Functions Continuous Functions  Properties of Continuous Functions Properties of Continuous Functions  Examples Examples  Example 4 Example 4 |
|
Last Update: 2006-11-15


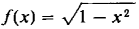 , a = -1, b = 1. Then f(-1) = f(1) = 0. The function f is continuous on [-1, 1] and has a derivative at each point of (-1,1), as Rolle's Theorem requires (Figure 3.8.14). Note, however, that f'(x) does not exist at either endpoint, x = -1 or x = 1. By Rolle's Theorem there is a point c in (-1, 1) such that f'(c) = 0, c = 0 is such a point, because
, a = -1, b = 1. Then f(-1) = f(1) = 0. The function f is continuous on [-1, 1] and has a derivative at each point of (-1,1), as Rolle's Theorem requires (Figure 3.8.14). Note, however, that f'(x) does not exist at either endpoint, x = -1 or x = 1. By Rolle's Theorem there is a point c in (-1, 1) such that f'(c) = 0, c = 0 is such a point, because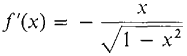 , f'(0) = 0.
, f'(0) = 0.