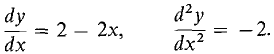The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Continuous Functions Derivatives and Curve Sketching Examples Example 2
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Example 2

Sketch the curve

y = 2x - x2.

03_continuous_functions-247.gif

We see that dy/dx = 0 when x = 1, a critical point. d2y/dx2 is never zero because it is constant. We make a table of values including the critical point x = 1 and points to the right and left of it.

x

y

03_continuous_functions-248.gif

03_continuous_functions-249.gif

-1

-3

4

-2

0

0

2

-2

1

1

0

-2

2

0

-2

-2

3

-3

-4

-2

CONCLUSIONS

(a) dy/dx > 0 for x < 1; increasing.

(b) dy/dx < 0 for x > 1; decreasing.

(c) d2y/d2x < 0 for all x; concave downward.

(d) dy/dx = 0, d2y/d2x < 0 at x = 1; maximum.

The curve is shown in figure 3.7.8.

03_continuous_functions-250.gif

Figure 3.7.8

Home Continuous Functions Derivatives and Curve Sketching Examples Example 2

Last Update: 2006-11-15