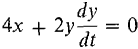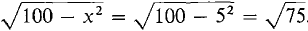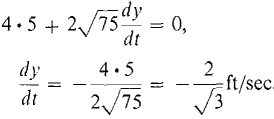| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Continuous Functions Continuous Functions  Related Rates Related Rates  Examples Examples  Example 2 Example 2 |
|||||||||






|
|||||||||
Example 2
A 10 foot ladder is propped against a wall. The bottom end is being pulled along the floor away from the wall at a constant rate of 2ft/sec. Find the rate at which the top of the ladder is sliding down the wall when the bottom end is 5 ft from the wall. Warning: The diagram is shown in Figure 3.2.2.
Figure 3.2.2
|
|||||||||
Home  Continuous Functions Continuous Functions  Related Rates Related Rates  Examples Examples  Example 2 Example 2 |
|||||||||
Last Update: 2006-11-15



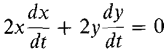 , whence
, whence