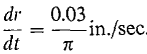| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Continuous Functions Continuous Functions  Related Rates Related Rates  Examples Examples  Example 1: Example 1: |
|||||||||||||






|
|||||||||||||
Example 1:
The point of a fountain pen is placed on an ink blotter, forming a circle of ink whose area increases at the constant rate of 0.03 in.2/sec. Find the rate at which the radius of the circle is changing when the circle has a radius of ½ inch. We solve the problem in four steps.
|
|||||||||||||
Home  Continuous Functions Continuous Functions  Related Rates Related Rates  Examples Examples  Example 1: Example 1: |
|||||||||||||
Last Update: 2006-11-15



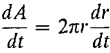 , whence
, whence 
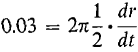 , so
, so