| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Continuous Functions Continuous Functions  Related Rates Related Rates  Examples Examples  Example 3 Example 3 |
|||||||||||||






|
|||||||||||||
Example 3
One car moves north at 40 mph (miles per hour) and passes a point P at time 1:00. Another car moves east at 60 mph and passes the same point P at time 2:30. How fast is the distance between the two cars changing at the time 2:00? It is not even easy to tell whether the two cars are getting closer or farther away at time 2:00. This is part of the problem.
|
|||||||||||||
Home  Continuous Functions Continuous Functions  Related Rates Related Rates  Examples Examples  Example 3 Example 3 |
|||||||||||||
Last Update: 2006-11-15



 x2 + y2 = z2.
x2 + y2 = z2.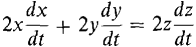 , whence
, whence 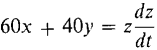
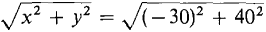 = 50.
= 50.  ,
,  -4.
-4.