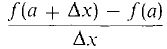Derivatives

We are now ready to explain what is meant by the slope of a curve or the velocity of a moving point Consider a real function f and a real number a in the domain of f. When x has value a, f(x) has value f(a). Now suppose the value of x is changed from a to a hyperreal number a + Δx which is infinitely close to but not equal to a. Then the new value of f(x) will be f(a + Δx). In this process the value of x will be changed by a nonzero infinitesimal amount Δx, while the value of f (x) will be changed by the amount

f(a + Δx) - f(a).

The ratio of the change in the value of f(x) to the change in the value of x is

This ratio is used in the definition of the slope of f which we now give.

The slope, when it exists, is infinitely close to the ratio of the change in f(x) to an infinitely small change in x. Given a curve y = f(x), the slope of f at a is also called the slope of the curve y = f(x) at x = a. Figure 2.1.1 shows a nonzero infinitesimal Δx and a hyperreal straight line through the two points on the curve at a and a + Δx. The quantity

is the slope of this line, and its standard part is the slope of the curve.