| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Differentiation Differentiation  Derivatives Derivatives  Existance of Slope Existance of Slope |
|






|
|
Existance of Slope
The slope of f at a does not always exist. Here is a list of all the possibilities. (1) The slope of f at a exists if the ratio
(2) The slope of f at a can fail to exist in any of four ways:
We can consider the slope of f at any point x, which gives us a new function of x. DEFINITION Let f be a real function of one variable. The derivative of f is the new function f' whose value at x is the slope of f at x. In symbols,
whenever the slope exists. The derivative f'(x) is undefined if the slope of f does not exist at x. For a given point a, the slope of f at a and the derivative of f at a are the same thing. We usually use the word "slope" to emphasize the geometric picture and "derivative" to emphasize the fact that f is a function. The process of finding the derivative of f is called differentiation. We say that f is differentiable at a if f'(a) is defined; i.e., the slope of f at a exists.
|
|
Home  Differentiation Differentiation  Derivatives Derivatives  Existance of Slope Existance of Slope |
|
Last Update: 2010-11-25


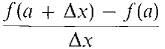

 is infinite for some infinitesimal Δx ≠ 0.
is infinite for some infinitesimal Δx ≠ 0. has different standard parts for different infinitesimals Δx ≠ 0.
has different standard parts for different infinitesimals Δx ≠ 0.