Problems

Compute the standard parts of the following.

In the following problems let a, b, a₁, b, be hyperreal numbers with a ≈ a₁, b ≈ b₁.

35            Show that a + b « a₁ + b₁.

Hint: Put a₁ = a + ε, b₁ = b + δ, and compute the difference (a₁ + b₁) - (a + b).

36            Show that if a, b are finite, then ab ≈ a₁ b₁.

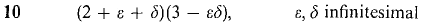
37            Show that if a = δ = H, a₁ = b₁ = H + 1/H, then ab a₁ b₁.(H positive infinite).