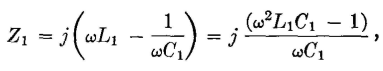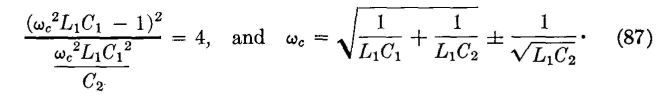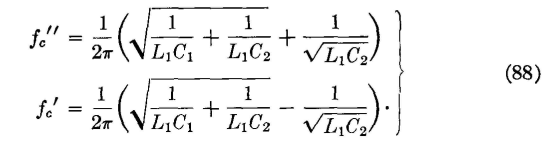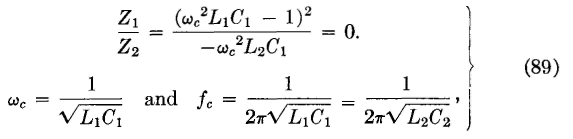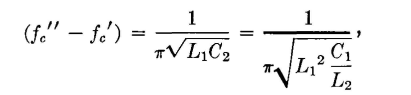Band-Pass Filter

Figure 34. Attenuation curves as calculated, using equation 84, and as measured. These curves are for one T section of the constant-k high-pass filter calculated on page 175. Small variations in the measured values above cutoff have been neglected.

Figure 35. Phase-shift curves for one T section of a constant-k high-pass filter as calculated by equation 85 and as measured as explained for Fig. 30. Constants calculated on page 175.

Figure 36. Reactance curves for a high-pass filter.

For the filter of Fig. 37,

and

The ratio Z₁/Z₂ (when L₁C₁ = L₂C₂, and L₂ = L₁C₁/C₂ are substituted) is

Figure 37. A band-pass filter of the constant-k type.

A network of this general type will pass frequencies between Z₁/Z₂ = -4 and Z₁/Z₂ = 0. Accordingly, equation 86 becomes

As equation 87 indicates, an upper and a lower cutoff frequency are obtained; that is,

and

These cutoff points were found by Z₁/Z₂ = -4. When the ratio is equated to zero,

Then,

since L₁C₁ = L₂C₂. This is not a true cutoff frequency,⁴ but lies at the middle of the band passed. It is the frequency for which the series arm is resonant and the shunt arm antiresonant as previously considered. In a generalized filter there are two bands passed; but with L₁C₁ = L₂C₂ these two bands "flow together" and the filter is of the simple confluent type. If the two expressions of equation 88 are subtracted,

since L₁C₁ = L₂C₂. Then,

where Z_K = sqrt(L₂/C₁) = sqrt(L₁/C₂) and is the iterative impedance taken at the resonant frequency. By making similar substitutions,

As an illustration of the design of a simple confluent constant-k band-pass filter, assume that it is desired to construct a filter such that Z_K = 600 ohms, f_c' = 900 cycles, and f_c" = 1100 cycles. Then,

The values here computed are for the entire series and parallel arms of Fig. 37. If a T section is desired, it should be constructed as indicated in Fig. 38. Also, the values for a π section may be readily determined.

Figure 38. A T section of a band-pass filter. Capacitance in microfarads. Inductance in millihenrys.

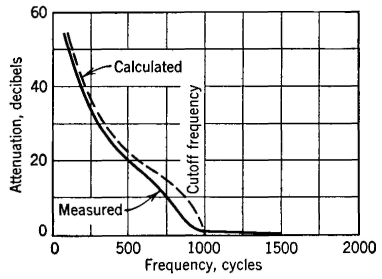
The attenuation curve for a band-pass filter of this type would be approximately as shown in Fig. 39.

The pass bands can also be computed by reactance sketches^4,5 as in Fig. 40. This sketch is not for the simple confluent type just considered. It will therefore be noted that -4Z₂ values determined by the parallel or antiresonant circuit do not pass through infinity at the same point that the Z₁ curve determined by the series elements passes through zero. The two transmission bands T and T' are accordingly not confluent and, as the diagram indicates, exist separately. This figure represents a double band-pass filter.