Synthese logischer Funktionen

Für die Diskussion in diesem Abschnitt werden die Eingänge einer logischen Schaltung mit Kleinbuchstaben bezeichnet (IN1 = a, IN2 = b, ...). Meist sind Problemstellungen für die eine bestimmte Schaltung gefunden werden soll, in Form einer Wahrheitstafel festgelegt. Bei der Synthese einer der Wahrheitstafel entsprechenden logischen Funktion geht man folgendermaßen vor:

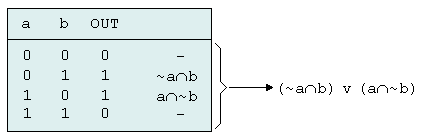
1) Man zählt die Nullen und Einsen in der Ausgangsspalte der Wahrheitstafel.
2) Überwiegt die Zahl der Nuller, so konstruiert man die 'disjunktive Normalform', andernfalls die 'konjunktive Normalform' (siehe unten).
3) Dieser Ausdruck wird nun durch Anwendung der Boole'schen Algebra vereinfacht. Bei der Vereinfachung benötigt man entweder viel Erfahrung oder man hat ein Computerprogramm zur Verfügung oder man verwendet sogenannte Karnaugh-Veitch-Diagramme.

Disjunktive Normalform

Zur Konstruktion der disjunktiven Normalform eines logischen Ausdrucks aus der Wahrheitstafel geht man so vor: Man konstruiert für jede Zeile der Wahrheitstafel in der eine Eins in der Ausgangsspalte steht, einen Term der alle Eingangsvariablen durch UND verbindet. Jene Eingangsvariablen, die in dieser Zeile eine Null haben, werden invertiert eingesetzt. Alle diese Terme werden durch ODER verbunden. Ein Beispiel soll das Verfahren veranschaulichen. Gegeben ist eine Wahrheitstafel die in einen logischen Ausdruck umgewandelt werden soll.

Disjunktive Normalform

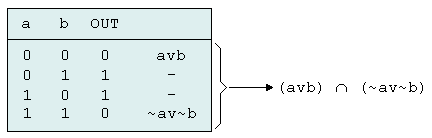
Die oben angeführte Wahrheitstafel kann also durch den logischen Ausdruck (~ab) v (a~b) beschrieben werden.

Konjunktive Normalform

Zur Konstruktion der konjunktiven Normalform eines logischen Ausdrucks geht man so vor: Man konstruiert für jede Zeile der Wahrheitstafel, in der eine Null in der Ausgangsspalte steht, einen Term der alle Eingangsvariablen durch ODER verbindet. Jene Eingangsvariablen, die in dieser Zeile eine Eins haben, werden invertiert eingesetzt. Alle diese Terme werden durch UND verbunden. Für das oben gezeigte Beispiel soll die konjunktive Normalform ermittelt werden.

Konjunktive Normalform

Die oben angeführte Wahrheitstafel kann also durch den logischen Ausdruck (avb) (~av~b) beschrieben werden. Konjunktive und disjunktive Normalform sind äquivalent.