| Electronic Transformers and Circuits is a free introductory textbook on transformers and related circuits. See the editorial for more information.... |

|

Home  Pulse and Video Transformers Pulse and Video Transformers  Pulse Transformers - Example Pulse Transformers - Example |
|||||||||||||||||||






|
|||||||||||||||||||
Pulse Transformers - Example
Pulse voltage ratio 2,000:10,000 volts. Pulse duration 2 microseconds. Pulse repetition rate 1,000 per second. Impedance ratio 50:1,250 ohms (linear). To rise to 90 per cent of final voltage in 1/4 microsecond or less. Droop not to exceed 10 per cent in 2 microseconds. Backswing amplitude not to exceed 60 per cent of pulse voltage. 50-ohm source.
The final design has the following:
Primary turns = 20. Secondary turns = 100. Core: 2-mil silicon steel with 1-mil gap per leg. Core area = 0.55 sq in. Core length = 6.3 in. (lg/lc = 0.0003). Core weight 0.75 lb, window 5/8 in. · 1 9/16 in. Primary leakage inductance = 2 microhenrys. Effective primary capacitance = 1,800 μμf. No-load loss equivalent to 400 ohms (referred to primary).
At 2 microseconds and B = 5,600 μ ≈ 600.
Front-edge performance is figured as follows:
According to Fig. 231, this value of k gives 90 per cent of Ea in 0.35T or 0.131 microsecond. The top is figured at
and from the curve R1 = R2 in Fig. 234, the top droops 9 per cent. The magnetizing current is (R1 + R2)/R1 · 9 per cent or 18 per cent of the load current. For the backswing
From Fig. 235, the backswing is 20 per cent of Ea. If the load resistance is connected to the transformer when the pulse voltage is removed, the backswing superposed oscillation has the same k (1.08) as the front edge, that is, there is no oscillation and the total backswing voltage is 20 per cent of Ea. Suppose the load were non-linear; the voltage would rise up to E within 1/4T or 0.094 microsecond. The front edge
and
k = 0.8 From Fig. 244,
The secondary effective capacitance is 1,800/25 = 72 μμf and the initial load current is
Final load current is 10,000/1,250 = 8 amp, and current is non-uniform during the pulse. The backswing is calculated in Pulse Circuits, Secondary current is 8 amp. The rms value of this current is, from Table I,
and the primary current is 5 · 0.36 = 1.8 amp. The wire insulation must withstand 10,000 / 100 = 100 volts per turn, and with single-layer windings this normally requires at least 0.0014 in. of covering insulation. Heavy enamel wire, No. 28, has a margin of insulation over this value. This is further modified by the initial non-uniform voltage distribution as figured below. A sectional view of a two-coil design is shown in Fig. 245, with No. 28 heavy enamel wire in the secondary and No. 22, wound two in parallel to occupy the form fully, in the primary.
The core section is 3/4 in. by 3/4 in. The primary turn length is 3.75 in. and that of the secondary is 4.13 in. Primary and secondary d-c resistances are 0.05 and 2.3 ohms, and the respective copper losses are
The no-load loss is [(2,000)2/400] · 1,000 · 2 · 10-6 = 20 watts. copper loss is therefore of little significance. From the coil dimensions and insulation thicknesses we can figure the capacitances. The total winding traverse for both coils is 1.875 in. The primary-to-core capacitance is
and the secondary-to-primary capacitance is
so that these two capacitances in series are 94 μμf. Secondary turn-to-turn capacitance is, approximately,
or
Cw = 0.184 α is therefore Figure 246 is a photograph of the transformer with Fosterite-treated coils.
|
|||||||||||||||||||
Home  Pulse and Video Transformers Pulse and Video Transformers  Pulse Transformers - Example Pulse Transformers - Example |
|||||||||||||||||||
Last Update: 2011-01-24


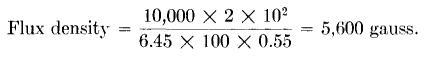













 = 22.5, and the wire enamel initially must withstand 2,250 volts per turn.
= 22.5, and the wire enamel initially must withstand 2,250 volts per turn.
