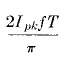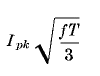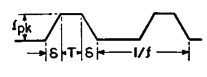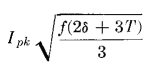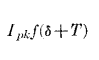Wave Shapes

Transformers in electronic circuits may be subjected to alternating and direct currents simultaneously, to modified sine waves, or to other non-sinusoidal waves. Although there is a relation between current and voltage wave shapes in a transformer, the two are frequently not the same, as has already been seen in Fig. 5. D-c components of primary voltage are not transformed; only the varying a-c component is transformed. Secondary current may be determined by the connection of the load. For example: if the load is a rectifier, the current will be some form of rectified wave; if the load is a modulator, the secondary current may be the superposition of two waves. If the primary voltage is non-sinusoidal, then the secondary current almost certainly will be non-sinusoidal.

If the primary voltage comes from an alternating source only, and the load is a half-wave rectifier, the secondary current has a d-c component, but the primary current has no d-c component except under changing conditions. That is to say, in the steady state there is no primary d-c component resulting from secondary d-c component alone. This is true, because any direct current in the primary requires a d-c source. But by the initial assumption there is no direct current present in the primary. Under these conditions, the core flux may be very much distorted because the flux excursions go into saturation in one direction only.

In succeeding chapters, two values of current will be of interest in circuits with non-sinusoidal waves, the average and the rms. Average current causes core saturation unless there is an air gap. Rms current determines the heating of the windings and is limited by the permissible temperature rise. Voltage wave form will be dealt with in subsequent chapters. Common current wave forms are tabulated here for convenience.

Table I. Non-Sinusoidal Current Wave Forms

Current Wave Shape	Description	Irms	Iav
	Direct current with superposed sine wave
	Half-sine loops of T duration and f repetition rate
	Square waves of T duration and f repetition frequency
	Sawtooth wave of T duration and f repetition frequency
	Trapezoidal wave of f repetition frequency

Root-mean-square or rms current values are based upon the equation

[17]

where

i = current at any instant
f = frequency of repetition of current waves per second
T = duration of current waves in seconds
t = time in seconds.

[18]

In the first wave shape, T = 1/f. In the fifth wave shape, T + 2δ is the current wave duration.

In both equations 17 and 18, T refers to a full period. This is in contrast to steady-state sinusoidal alternating currents, the rms and average values of which are developed over a half-period because of the symmetry of such currents about the zero axis.