| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Surface Area and Surface Integrals Surface Area and Surface Integrals  Area Of A Smooth Surface Area Of A Smooth Surface |
|






|
|
Area Of A Smooth Surface
In Chapter 6 we were able to find the area of a surface of revolution by a single integral. To find the area of a smooth surface in general (Figure 13.5.1), we need a double integral. We call a function f(x, y), or a surface z = f(x, y), smooth if both partial derivatives of f are continuous.
Figure 13.5.1 DEFINITION The area of a smooth surface z = f(x, y), (x, y) in D is
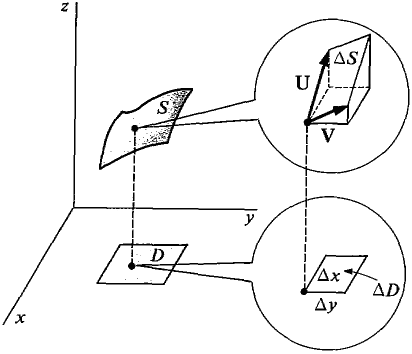
JUSTIFICATION Let S(D1) be the area of the part of the surface with (x, y) in Dv S(D1) has the Addition Property, and S(D1) ≥ 0. Consider the piece of the surface ΔS above an element of area ΔD (Figure 13.5.2). ΔS is infinitely close to the piece of the tangent plane above ΔD, which is a parallelogram with sides
Figure 13.5.2 The quickest way to find the area of this parallelogram is to use the vector product formula (Section 10.4, Problem 39), Area = |U x V|. Then Therefore
and by the Infinite Sum Theorem,
|
|
Home  Vector Calculus Vector Calculus  Surface Area and Surface Integrals Surface Area and Surface Integrals  Area Of A Smooth Surface Area Of A Smooth Surface |
|
Last Update: 2010-11-25




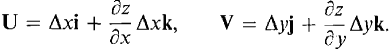
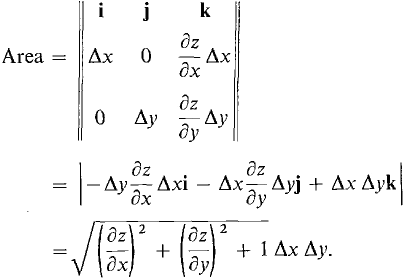
 (compared to Δx Δy),
(compared to Δx Δy),