| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Vector Calculus Vector Calculus  Green's Theorem Green's Theorem  Problems Problems |
|






|
|
Problems
In Problems 1-12, find the line integral by Green's Theorem.
In Problems 13-18, find (a) curl F, (b)
19 Use Green's Theorem to find the area inside the curve r = a + cos θ, (α ≥ 1). 20 Use Green's Theorem to find the area inside the ellipse x2/a2 + y2/b2 = 1 and above the line y = c (0 < c < b). 21 Show that if D has a piecewise smooth boundary, the area of D is 22 Show that for any continuous function f(t) and constants a, b, c, 23 Find the value of the line integral where D is a region with area A. 24 Show that any vector field of the form F(x,y) = xf(x2 + y2)i + yf(x2 + y2)j is irrotational. 25 Show that any vector field of the form F(x, y) = y f(x2 + y2)i - xf(x2 + y2)j is incompressible. 26 Show that any vector field of the form F(x,y) = f(x)i + g(y)j is irrotational.
|
|
Home  Vector Calculus Vector Calculus  Green's Theorem Green's Theorem  Problems Problems |
|
Last Update: 2006-11-25






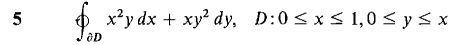






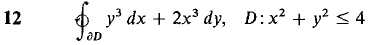
 (c) div
(c) div 



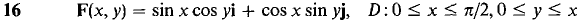



 where D is the circle x2 + y2 ≤ c2.
where D is the circle x2 + y2 ≤ c2.