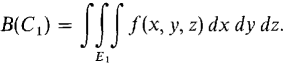| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |
|
Home  Multiple Integrals Cylindrical and Spherical Coordinates Examples Example 2 |
|||||||
 Search the VIAS Library | Index
|
  |
||||||
Example 2
Find the center of mass of a cone of constant density with height h and base a circle of radius b.
Figure 12.7.11 To express a point P(x, y, z) in spherical coordinates we let ρ (rho) be the distance from the origin to P, let θ be the same angle as in cylindrical coordinates, and let φ be the angle between the positive z-axis and the line OP. Note that φ can always be chosen between 0 and n.
Figure 12.7.12 We see from Figure 12.7.12 that a point (x, y, z) has spherical coordinates (θ, φ, ρ) if x = ρ sin φ cos θ, y = ρ sin φ sin θ, z = ρ cos θ. The graph of the equation ρ = constant is a sphere with center at the origin (hence the name spherical coordinates). The graph of φ = constant is a vertical cone with vertex at the origin. The graph of θ = constant is a half-plane through the z-axis. These surfaces are shown in Figure 12.7.13.
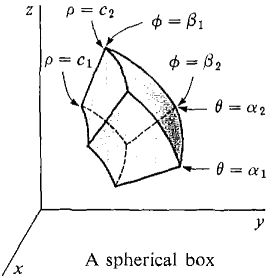
Figure 12.7.13 DEFINITION A spherical region E is a region in (x, y, z) space given by spherical coordinate inequalities α1 ≤ θ ≤ α2, β1(θ) ≤ φ ≤ β2(θ), c1(θ, φ) ≤ ρ ≤ c2(θ, φ), where all the functions are continuous. To avoid overlaps we also require that for (θ, φ, ρ) in E, 0 ≤ θ ≤ 2π, 0 ≤ φ ≤ π, 0 ≤ ρ. A spherical box is a spherical region of the simple form α1 ≤ θ ≤ α2, β1 ≤ φ ≤ β2, c1 ≤ ρ ≤ c2. The θ-boundaries are planes, the θ-boundaries are portions of cone surfaces, and the ρ-boundaries are portions of spherical surfaces. Figure 12.7.14 shows a spherical box.
Figure 12.7.14 The spherical box 0 ≤ θ ≤ 2π, 0 ≤ φ ≤ π, 0 ≤ ρ ≤ c is a sphere of radius c with center at the origin. The spherical box 0 ≤ θ ≤ 2π, 0 ≤ φ ≤ β, 0 ≤ ρ ≤ c is a cone whose vertex is at the origin and whose top is spherical instead of flat. (See Figure 12.7.15.)
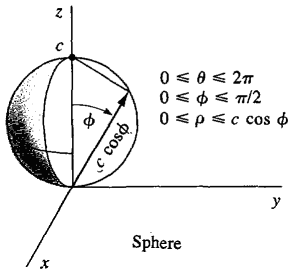
Figure 12.7.15 Another important example is the spherical region 0 ≤ 0 ≤ 2π, 0 ≤ φ ≤ π/2, 0 ≤ ρ ≤ c cos φ, which is a sphere of radius ½c whose center is on the z-axis at z = ½c (Figure 12.7.16).
Figure 12.7.16 When integrating over a solid region E made up of spheres or cones, it is often easiest to use spherical coordinates. SPHERICAL INTEGRATION FORMULA Let E be a spherical region α1 ≤ 0 ≤ α2, β1 ≤ φ ≤ β2(θ), cl(θ,φ) ≤ ρ ≤ c2 (θ, φ). The triple integral of f(x, y, z) over E is
In practice we make the substitution f(x, y, z) = f(ρ sin φ cos θ, ρ sin φ sin θ, ρ cos φ) before integrating. PROOF Let C be the region in the rectangular (θ, φ, ρ) space which has the same inequalities as E. We prove
As usual we let f(x, y, z) > θ on E and put
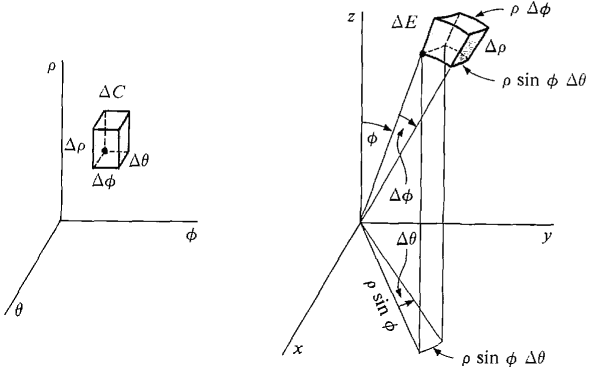
Figure 12.7.17 Spherical Element of Volume Consider an element of volume ΔC. As we see from Figure 12.7.17, ΔC corresponds to a spherical box ΔE. ΔE is almost a rectangular box with sides Δρ, ρ Δφ, ρ sin (φ) Δθ and volume ρ2 sin φ Δθ Δφ Δρ. Thus B(ΔC) ≈ f(x, y, z)ρ2 sin φ Δθ Δφ Δρ (compared to Δθ Δφ Δρ). By the Infinite Sum Theorem
and by definition
The triple integral for volume,
gives us iterated integral formulas for volume in rectangular, cylindrical, and spherical coordinates. Rectangular Cylindrical Spherical The rectangular formula is really equivalent to the double integral for the volume between two surfaces. Similarly, the cylindrical formula is equivalent to the double integral in polar coordinates for the volume between two surfaces. On the other hand, the volume formula in spherical coordinates is something new which is useful for finding volumes of spherical regions.
|
|||||||
| Home Multiple Integrals Cylindrical and Spherical Coordinates Examples Example 2 |
|
||||||
Last Update: 2010-11-25