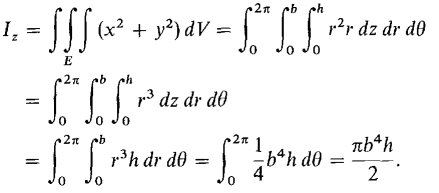| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Multiple Integrals Multiple Integrals  Cylindrical and Spherical Coordinates Cylindrical and Spherical Coordinates  Examples Examples  Example 1 Example 1 |
|||||||






|
|||||||
Example 1
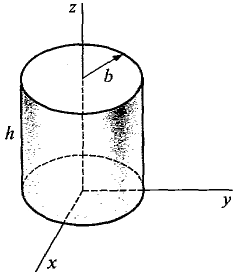
Find the moment of inertia of a cylinder of height h, base a circle of radius b, and constant density 1, about its axis.
Figure 12.7.9
|
|||||||
Home  Multiple Integrals Multiple Integrals  Cylindrical and Spherical Coordinates Cylindrical and Spherical Coordinates  Examples Examples  Example 1 Example 1 |
|||||||
Last Update: 2006-11-15


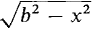 ≤y≤
≤y≤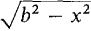 , 0≤z≤h, and in cylindrical coordinates is 0 ≤ 0 ≤ 2π, 0≤r≤b, 0 ≤ z ≤ h.
, 0≤z≤h, and in cylindrical coordinates is 0 ≤ 0 ≤ 2π, 0≤r≤b, 0 ≤ z ≤ h.