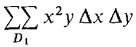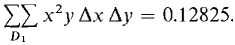The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Multiple Integrals Double Integrals Examples Example 1
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

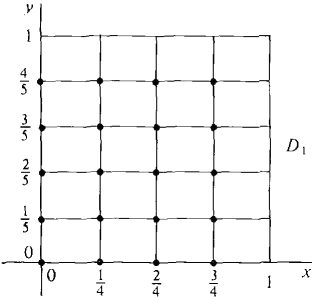
Example 1

Find the double Riemann sum

12_multiple_integrals-19.gif

where D1 is the square

0 ≤ x ≤ 1, 0 ≤ y ≤ 1,

and

Δx = ¼, Δy = 1/5.

The partition of D1 is shown in Figure 12.1.10 and the values of x2y at the partition points are shown in the table.

12_multiple_integrals-22.gif

Figure 12.1.10

x2y

y0 = 0

y1 = 1/5

y2 = 2/5

y3 = 3/5

y4 = 4/5

x0 = 0

0

0

0

0

0

x1 = ¼

0

1/80

2/80

3/80

4/80

x2 = ½

0

4/80

8/80

12/80

16/80

x3 = ¾

0

9/80

18/80

27/80

36/80

The double Riemann sum is

12_multiple_integrals-20.gif

= (1 + 2 + 3+ 4 + 4 + 8 + 12 + 16 + 9 + 18 + 27 + 36)1/80 · ¼ · 1/5 = 0.0875.

A similar computation with Δx = 1/10, Δy = 1/10 gives

12_multiple_integrals-21.gif

 

 

 
Home Multiple Integrals Double Integrals Examples Example 1

Last Update: 2010-11-25