| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Implicit Functions Implicit Functions  Implicit Functions Implicit Functions |
|||||






|
|||||
Implicit Functions
In many applications of the Chain Rule, one or more of the independent variables is also used as an intermediate variable. The simplest case where this occurs is when z depends on x and y while y depends on x, y = g(x), z = F(x, y). Figure 11.6.1 shows which variables depend on which.
Figure 11.6.1 Assuming F(x, y) is smooth and dy/dx = g'(x) exists, the Chain Rule gives
Here dz/dx stands for f'(x) where z = f(x) = F(x, g(x)), and ∂z/∂x stands for Fx(x, y). The round d, ∂, is useful in telling the two apart.
In many problems we are given a relationship between x and y which can be expressed by an equation of the form F(x, y) = 0, and we wish to find dy/dx. The graph of F(x, y) = 0 is usually a curve in the (x, y) plane. If we put z = F(x, y) = 0, then dz/dx = 0 while dy/dx is the slope of the curve. Ordinarily such a curve can be divided into finitely many pieces each of which is the graph of a function y = g(x). For example, the top and bottom halves of the circle x2 + y2 - 1 = 0 are the functions y = shown in Figure 11.6.2.
Figure 11.6.2 DEFINITION An implicit function of the curve F(x, y) = 0 at (a, b) is a function y = g(x) such that:
If every implicit function of F(x, y) = 0 has the same slope S at (a, b), we call S the slope of the curve.
Figure 11.6.3 Figure 11.6.3 shows an implicit function y = g(x) of a curve F(x,y) = 0. It is often hard or impossible to express an implicit function in terms of known (or elementary) functions. However, the next theorem gives an easy test for showing that there is an implicit function and finding its slope.
|
|||||
Home  Partial Differentiation Partial Differentiation  Implicit Functions Implicit Functions  Implicit Functions Implicit Functions |
|||||
Last Update: 2006-11-25





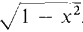 y =
y = 



