| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Partial Differentiation Partial Differentiation  Chain Rule Chain Rule  Problems Problems |
|






|
|
Problems
In Problems 1-6, calculate dz/dt by the Chain Rule and check by a direct calculation.
In Problems 7-14, calculate dz/dt by the Chain Rule.
In Problems 15-20, find ∂z/∂s and ∂z/∂t by the Chain Rule.
21 If z = f(ax + by) and f is differentiable, show that 22 If z = f(x + at,y + bt) and f is smooth, show that
23 If z = f(x, y), x = r cos θ, y = r sin θ, and f is smooth, show that
24 If z = f 25 Find dw/dt where w = x cos z + y sin z, x = et, y = e-t, z = √t. 26 Find dw/dt where w = xy2z3, x = 2t + 1, y = 3t - 2, z = 1 - 4t. In Problems 27-30, find formulas for dz/dt.
In Problems 31-36, find formulas for ∂z/∂s and ∂z/∂t.
37 A particle moves in the (x, y) plane so that dx/dt = 2, dy/dt = -4. Find dz/dt, where z is the distance from the origin, when the particle is at the point (3,4). 38 A particle moves in the (x, y) plane so that
Find dz/dt, where z is the distance of the particle from the point (1,2), when the particle is at (2,3). 39 A particle moves in space so that
Find the rate of change of the distance from the origin when x = 1, y = -2, z = 2. 40 Find the rate of change of the area of a rectangle when the sides have lengths x = 5 and y = 6 and are changing at rates dx/dt = 3, dy/dt = -4. 41 Find the rate of change of the perimeter of a rectangle when the sides are x = 2, y = 4 and are changing at the rates dx/dt = -2, dy/dt = 3. 42 The per capita income of a country is equal to the national income x divided by the population y. Find the rate of change in per capita income when x = $10 billion, y = 10 million, dx/dt = $10 million per year, dy/dt = 50,000 people per year. 43 The profit of a manufacturer is equal to the total revenue x minus the total cost y. As the number of items produced, u, is increased, the revenue and cost increase at the rates dx/du = 500/u and dy/du = 1/√u. Find the rate of increase of profit with respect to u when u = 10,000. 44 When commodities one and two have prices p and q respectively, their respective demands are D1(p, q) and D2(p, q). The revenue at prices p and q is the quantity R(p, q) = pD1(p,q) + qD2(p,q), since a quantity Dx(p, q) can be sold at price p and a quantity D2(p, q) at price q. Find formulas for the partial marginal revenues with respect to price, ∂R/∂p and ∂R/∂q.
|
|
Home  Partial Differentiation Partial Differentiation  Chain Rule Chain Rule  Problems Problems |
|
Last Update: 2006-11-25







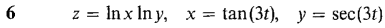




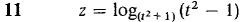

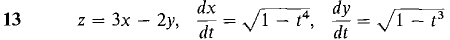








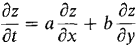

 , where f is differentiable,
, where f is differentiable, show that
show that