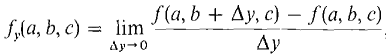Partial Derivatives of Functions of Three or More Variables

Functions of three or more variables cannot easily be represented graphically. However, they can be given other physical interpretations. For example,

w = f(x, y, t)

may be pictured as a moving surface in (x, y, w) space where f is time. Alternatively,

w = f(x, y, z)

may be thought of as assigning a number to each point of (x, y, z) space where it is defined; for example, w could be the density of a three-dimensional object at the point (x, y, z).

Partial derivatives of functions of three or more variables are defined in a manner analogous to the two-variable case.

When f_x(a, b, c) exists we have

for nonzero infinitesimal Δx.

Thus f_x (x, y, z) is the rate of change of f(x, y, z) with respect to x when y and z are held constant.

We also use the round d notation. If w = f(x, y, z), we use:

Example 3