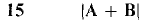Problems

In Problems 1-3, find the vector represented by the directed line segment

In Problems 4-6, find the point Q such that A is the vector from P to Q.

In Problems 7-22, find the given vector or scalar where

A = i - 2j + 2k, B = 2i + 3j - 6k

17            The angle between A and B

18            The angle between A and A + B

19            The angle between A and 3A

20            The angle between A and -2A

21             The unit vector and direction cosines of A

22            The unit vector and direction cosines of B

23             Find the vector with length 6 and direction cosines (-1/2, 1/2, 1/√2).

24             Find the vector with length √3 and direction cosines (1/√3, 1/√3, 1/√3).

25             If ⅓ and ⅔ are two of the direction cosines of a vector, what are the two possible values for the third direction cosine?

26             If the three forces F₁ = i + 2j + 3k, F₂ = 3i - j - k, F₃ = 4k are acting on an object, find the total force.

27             If a force F = 6i - 10j + 2k is acting on an object of mass 20, find its acceleration vector.

28            If a trader has the initial commodity vector A = 15i + 20j + 30k and buys the commodity vector B = 2i + k, find his new commodity vector.

29            If three commodities have the original price vector. P = 100i + 200j + 500k and all prices increase 25%, find the new price vector.

In Problems 30-35, find a vector equation for the given line.

30            The line with parametric equations x = - t, y = 1 + √2t, z - 6 - 8t.

31            The line with parametric equations x = 1 + t, y = 3, z = 1 - t.

32            The line through the points P(0,0,0), Q(l, 2, 3).

33            The line through the points P(-1, 4, 3), Q(-2, - 3, 6).

34            The line through the point P(4, 4, 5) with direction cosines (1/√6, √2/√6, √3/√6).

35            The line through the origin with direction cosines (-3/5, 0, 4/5).

36            Find the midpoint of the line segment AB where A = (- 6, 3,1), B = (0, - 4, 0).

37            Find the midpoint of AB where A = (1, 2, 3), B = (-1, 2, 7).

38            Find the midpoint of AB where A = (6, 8,10), B = (-6, -8, - 10).

39            Prove that if two sides of a triangle in space have equal lengths, then the angles opposite them are equal.

40            Prove that if θ is the angle between A and B then π - θ is the angle between A and -B. Hint: Show that the sum of the cosines is zero.

41            Prove the Triangle Inequality for three dimensions.

42            Use the Triangle Inequality to prove that if A and B are two nonzero vectors then