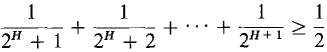| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Infinite Series Infinite Series  Series Series  Diverging Geometric Series (Theorem 2) Diverging Geometric Series (Theorem 2) |
|||||||||||






|
|||||||||||
Theorem 2: Diverging Geometric Series
The Cauchy Convergence Criterion and its corollary can often be used to show that a series diverges. Table 9.2.2 sums up the various possibilities. In this table it is understood that a1 + a2 + ... + an + ... is an infinite series and H, K are positive infinite hyperintegers with H < K.
We shall give many other convergence tests later on in this chapter. For convenience there is a summary of all these tests at the end of Section 9.6. THEOREM 2 (i) If |c| ≥ 1 the geometric series 1 + c + c2 + ... + cn + ... diverges. (ii) The harmonic series PROOF (i) For infinite H the term cH is not infinitesimal, so the series diverges, (ii) Intuitively this can be seen by writing
Instead we can use the Cauchy Test. We see that for each n,
Therefore for infinite H,
Since the above sum is not infinitesimal the series diverges. example 3 The harmonic series
is the example promised in our warning. It has the property that
and yet the series diverges.
|
|||||||||||
Home  Infinite Series Infinite Series  Series Series  Diverging Geometric Series (Theorem 2) Diverging Geometric Series (Theorem 2) |
|||||||||||
Last Update: 2006-11-08


 0
0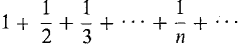 diverges.
diverges.