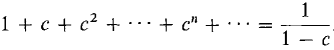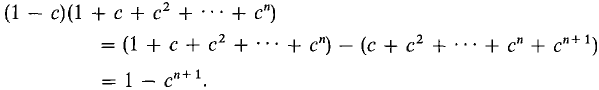The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Infinite Series Series Theorem 1: Converging Geometric Series
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 1: Converging Geometric Series

Our next theorem gives a formula for the sum of an important kind of series, the geometric series.

For each constant c, the series

1 + c + c2 + ... + cn + ... is called the geometric series for c.

THEOREM 1

If |c| < 1, the geometric series converges and

09_infinite_series-68.gif

PROOF

For each n we have

09_infinite_series-69.gif

The nth partial sum is therefore

09_infinite_series-70.gif

The infinite partial sum up to H is

09_infinite_series-71.gif

Since |c| < 1, cH+l is infinitesimal, so

09_infinite_series-72.gif

Example 1
Example 2: Partial Sum Sequence

The Cauchy Convergence Test from the preceding section takes on the following form for series.

CAUCHY CONVERGENCE TEST FOR SERIES

a1 + a2 + ... + an + ... converges if and only if (1) for all infinite H < K, aH+1 + aH+2 + ... + aK a 0.

DISCUSSION

The sum in (1) is just the difference in partial sums,

aH+1 + aH+2 + ... + aK = SK - SH.

A very important consequence of the Cauchy Convergence Criterion is that all the infinite terms of a convergent series must be infinitesimal. We state this consequence as a corollary, which is illustrated in Figure 9.2.1.

09_infinite_series-78.gif

Figure 9.2.1

COROLLARY

If the series a1 + a2 + ... + an + ... converges, then limn→∞ an - 0. That is, aK ≈ 0 for every infinite K.

PROOF

This is true by the Cauchy Criterion, with K = H + 1.

Warning: The converse of this corollary is false. It is possible for a sequence to have limn→∞ an = 0 and yet diverge. We shall give an example later (Example 3).
Home Infinite Series Series Theorem 1: Converging Geometric Series

Last Update: 2006-11-07