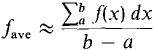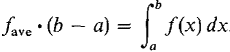Average Value

Given n numbers y_l, ..., y_n, their average value is defined as

.

If all the y_i are replaced by the average value y_ave, the sum will be unchanged,

y₁ + ... + y_n = y_ave + ... + y_ave = ny_ave.

If f is a continuous function on a closed interval [a, b], what is meant by the average value of f between a and b (Figure 6.5.1)?

Figure 6.5.1

Let us try to imitate the procedure for finding the average of n numbers. Take an infinite hyperreal number H and divide the interval [a, b] into infinitesimal subintervals of length dx = (b - a)/H. Let us "sample" the value of f at the H points a, a + dx, a + 2 dx, ..., a + (H - 1) dx. Then the average value of f should be infinitely close to the sum of the values of f at a, a + dx, ..., a + (H - 1) dx, divided by H. Thus

Since

,

and we have

Taking standard parts, we are led to

Geometrically, the area under the curve y = f(x) is equal to the area under the constant curve y = f_ave between a and b,

Example 1: Finding Average Value