| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Problems Problems |
|






|
|
Problems
In Problems 1-12, find the area of the surface generated by rotating the given curve about the y-axis.
In Problems 13-20, find the area of the surface generated by rotating the given curve about the x-axis.
21 The part of the circle x2 + y2 = r2 between x = 0 and x = a in the first quadrant is rotated about the x-axis. Find the area of the resulting zone of the sphere (0 < a < r). 22 Solve the above problem when the rotation is about the y-axis. In Problems 23-26 set up integrals for the areas generated by rotating the given curve about (a) the y:-axis, (b) the x-axis.
27 Set up an integral for the area generated by rotating the curve y = jx2, 0 < x < 1 about the x-axis and find the Trapezoidal Approximation with Δx = 0.2. 28 Set up an integral for the area generated by rotating the curve y = jx3, 0 < x < 1 about the y-axis and find the Trapezoidal Approximation with Δx = 0.2. 29 Show that the surface area of the torus generated by rotating the circle of radius r and center (c, 0) about the y-axis (r < c) is A = 4π2rc. Hint: Take y as the independent variable and use the formula
|
|
Home  Applications of the Integral Applications of the Integral  Area of a Surface of Revolution Area of a Surface of Revolution  Problems Problems |
|
Last Update: 2010-11-25







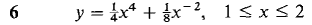





 first quadrant
first quadrant




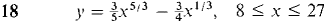






 for the length of the arc of the circle from y = a to y = b.
for the length of the arc of the circle from y = a to y = b.