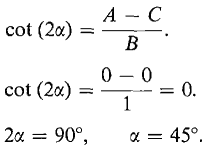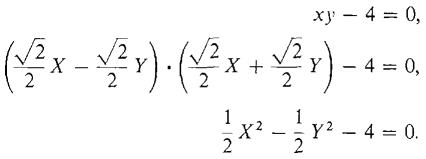The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Limits, Analytic Geometry, and Approximations Rotation of Axes Examples Example 2
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

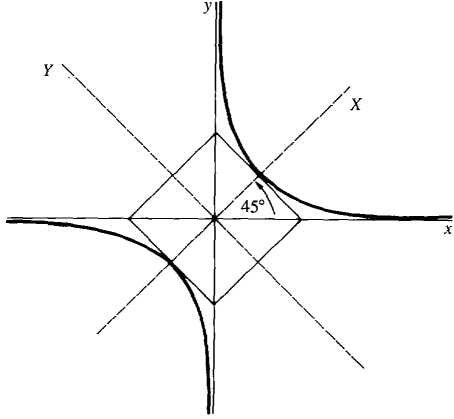
Example 2

Sketch the curve xy - 4 = 0.

Step 1

Apply the Discriminant Test to find the type of curve.

B2 - 4AC = 12 - 4 · 0 · 0 = 1.

The discriminant is positive, so the curve is a hyperbola.
Step 2

Find an angle α with

05_limits_g_approx-377.gif
Step 3

Change coordinate axes using the rotation equations.

05_limits_g_approx-378.gif

Substituting, we get

05_limits_g_approx-380.gif

As a check, the discriminant is still 02 - 4 · (½) · ( - ½) = 1.
Step 4

Draw the X and Y axes as dotted lines and sketch the curve.

The new axes are found by rotating the old axes by α = 45°. The curve is shown in Figure 5.7.5.

05_limits_g_approx-381.gif

Figure 5.7.5: Example 2: xy - 4 = 0
Home Limits, Analytic Geometry, and Approximations Rotation of Axes Examples Example 2

Last Update: 2006-11-15