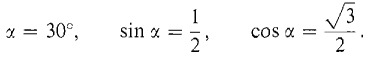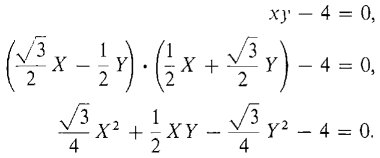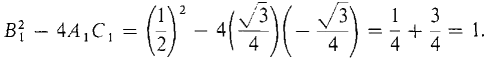Example 1

Find the equation of the curve

xy - 4 = 0,

with respect to the new coordinate axes X and Y formed by a counterclockwise rotation of 30 degrees (Figure 5.7.3).

Figure 5.7.3

In this example,

Thus

Substitute into the original equation and collect terms.

Given any second degree equation

(1)

Ax² + Bxy + Cy² + Dx + Ey + F = 0

and any angle of rotation a, one can substitute the equations of rotation and collect terms to get a new second degree equation in the X and Y coordinates,

(2)

A₁X² + B₁XY + C₁Y² + D₁X + E₁Y + F₁ = 0.

It can be shown that the discriminant is unchanged by the rotation; that is,

B² - 4AC = B₁² - 4A₁C₁.

This gives a useful check on the computations.

In Example 1 above, the original discriminant is

B² - 4AC = 1² - 4 · 0 · 0 = 1.

The new equation has the same discriminant,

The trouble with Example 1 is that the new equation is more complicated than the original equation, and in particular there is still a nonzero XY-term. We would like to be able to choose the angle of rotation α so that the new equation has no XY-term, because we could then sketch the curve. The next theorem tells us which angle of rotation is needed.