| The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages. |

|

Home  Integral Integral  Integration by Change of Variables Integration by Change of Variables  THEOREM 2 (Definite Integration by Change of Variables) THEOREM 2 (Definite Integration by Change of Variables) |
|||






|
|||
THEOREM 2 (Definite Integration by Change of Variables)
THEOREM 2 (Definite Integration by Change of Variables) Suppose I and J are open intervals, f is continuous and has an antiderivative on I, g has a continuous derivative on J, and g maps J into I. Then for any two points a and b in J,
PROOF Let F be an antiderivative of f. Then by Theorem 1, H(x) = F(g(x)) is an antiderivative of h(x) = f(g(x))g'(x). Since f, g, and g' are continuous, h is continuous on J. Then by the Fundamental Theorem of Calculus,
Example 5 shows us that
Figure 4.4.2
|
|||
Home  Integral Integral  Integration by Change of Variables Integration by Change of Variables  THEOREM 2 (Definite Integration by Change of Variables) THEOREM 2 (Definite Integration by Change of Variables) |
|||
Last Update: 2006-11-10



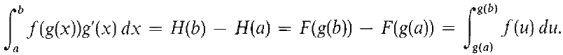

 that is, the areas shown in Figure 4.4.2 are the same.
that is, the areas shown in Figure 4.4.2 are the same.