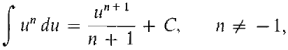Elementary Calculus: Integration by Change of Variables

We have seen that the sum, constant, and power rules for differentiation can be turned around to give the sum, constant, and power rules for integration. In this section we shall show how to make use of the Chain Rule for differentiation in problems of integration. The Chain Rule will lead to the important method of integration by change of variables. The basic idea is to try to simplify the function to be integrated by changing from one independent variable to another.

If F is an antiderivative of f and we take u as the independent variable, then

f(u) du is a family of functions of u,

But if we take x as the independent variable and introduce u as a dependent variable u = g(x), then du and

f(u) du mean the following:

The notation

f(u) du always stands for a family of functions of the independent variable, which in some cases is another variable such as x. The next theorem can be used as follows. To integrate a given function of x, properly choose a new variable u = g(x) and integrate a new function with respect to u.

DEFINITION

Let I and J be intervals. We say that a function g maps J into I if for every point x in J, g(x) is defined and belongs to I (Figure 4.4.1).

THEOREM 1 (Indefinite Integration by Change of Variables)

Suppose I and J are open intervals, f has domain I, g maps J into I, and g is differentiable on J. Assume that when we take u as the independent variable,

f(u)du = F(u) + C.

Then when x is the independent variable and u = g(x),

f(u) du = F(g(x)) + C.

PROOF

Let H(x) = F(g(x)). For any x in J, the derivatives g'(x) and F'(g(x)) = f(g(x)) exist. Therefore by the Chain Rule,

H'(x) = F(g(x))g'(x) = f (g(x))g'(x).

It follows that

f(g(x))g'(x)dx = H(x) + C = F(g(x)) + C.

So when u = g(x), we have

(u) du = f(g(x))g'(x) dx, f(u) du = F(g(x)) + C.

Theorem 1 gives another proof of the general power rule

where u is given as a function of the independent variable x, from the simpler power rule

where x is the independent variable.

In examples such as the above one, the trick is to find a new variable u such that the expression becomes simpler when we change variables. This usually must be done by an "educated" trial and error process.

One must be careful to express dx in terms of du before integrating with respect to u.