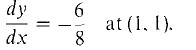Example 5

Find the slope of the line tangent to the curve

(4)

x⁵y³ + xy⁶ = y + 1

at the points (1,1), (1, -1), and (0, -1).

The three points are all on the curve, and the first two points have the same x coordinate, so Equation 4 does not by itself determine y as a function of x.

We differentiate with respect to x,

and then solve for dy/dx,

(5)

Substituting,

Equation 5 for dy/dx is true of any system S of formulas which contains Equation 4 and determines y as a function of x.

Here is what generally happens in the method of implicit differentiation. Given an equation

(6) 

τ(x,y) = σ(x,y)

between two terms which may involve the variables x and y, we differentiate both sides of the equation and obtain

(7)

We then solve Equation 7 to get dy/dx equal to a term which typically involves both x and y. We can conclude that for any system of formulas which contains Equation 6 and determines y as a function of x. Equation 7 is true. Also, Equation 7 can be used to find the slope of the tangent line at any point on the curve τ(x, y) = σ(x, y).