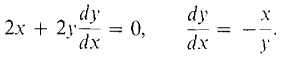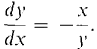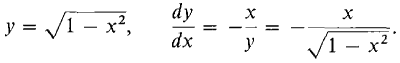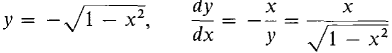Example 4

Given

(2)

x² + y² = 1,

find dy/dx. This equation does not determine y as a function of x; its graph is the unit circle. Nevertheless we differentiate both sides with respect to x and solve for dy/dx.

We can conclude that for any system of formulas S which contains the Equation 2 and also determines y as a function of x, it is true that

(3)

We can use Equation 3 to find the slope of the line tangent to the unit circle at any point on the circle. The following examples are illustrated in Figure 2.8.3.

The system of formulas

x² + y² = 1, y ≥ 0

gives us

On the other hand the system

x² + y² = 1, y ≤ 0

gives us