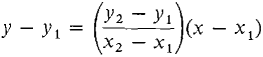The ebook Elementary Calculus is based on material originally written by H.J. Keisler. For more information please read the copyright pages.

Home Real and Hyperreal Numbers Straight Lines Theorem 1: Slope Of a Line
 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter Search the VIAS Library  |  Index

Theorem 1: Slope Of a Line

THEOREM 1

Suppose a line L passes through two distinct points P(x1,y1) and Q(x2,y2). If x1 = x2, then the line L is vertical. If x1 ≠ x2, then the slope of the line L is equal to the change in y divided by the change in x,

01_real_and_hyperreal_numbers-65.gif

PROOF

Suppose x1 ≠ x2, so L is not vertical. Let m be the slope of L. L has the point-slope formula

y - y1 = m(x - x1).

Substituting y2 for y and x2 for x, we see that

m = (y2 - y1)/(x2 - x1).

Theorem 1 shows why the slope of a line is a measure of its direction. Sometimes Δx is called the run and Δy the rise. Thus the slope is equal to the rise divided by the run. A large positive slope means that the line is rising steeply to the right, and a small positive slope means the line rises slowly to the right. A negative slope means that the line goes downward to the right. These cases are illustrated in Figure 1.3.4.

01_real_and_hyperreal_numbers-66.gif

Figure 1.3.4

There is exactly one line L passing through two distinct points P(x1,y2) and Q(x2, y2). If x1 ≠ x2, we see from Theorem 1 that L has the equation

01_real_and_hyperreal_numbers-67.gif

This is called the two-point equation for the line.
Home Real and Hyperreal Numbers Straight Lines Theorem 1: Slope Of a Line

Last Update: 2010-11-25