Receiver Characteristics with Diaphragm Blocked

Resistance and reactance curves obtained with the diaphragm of a telephone receiver blocked are as shown in Fig. 26. The test current for this figure and those that follow was 1.0 milliampere.

Figure 26. Resistance and reactance curves with diaphragm blocked.

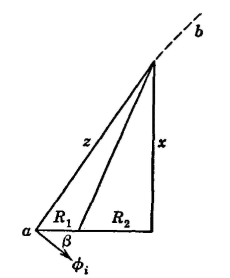
An impedance diagram corresponding to these readings is included in Fig. 27. The line R₁ represents the direct-current resistance of the receiver windings. The line R₂ represents that part of the total effective resistance due to power consumed largely in hysteresis and eddy-current losses in the magnetic circuit. The line R₁ + R₂ is the resistance component, the line x the reactive component, and z the impedance of the receiver with the diaphragm blocked. The corresponding vector diagram is given in Fig. 28. The vector E_z represents the voltage across the receiver, leading the receiver current I by an angle α. The vector φi is the flux produced by the current I and lags I by the angle β because of the hysteresis and the skin effect in the magnetic circuit.³³

Figure 27. Impedance diagram with diaphragm blocked.

The reactance of Fig. 27 increases almost directly as the frequency. The alternating-current portion R₂ of the damped receiver resistance is largely composed of hysteresis and eddy-current losses. Because of these losses the measured effective resistance varies as the frequency to some power greater than unity (page 52), and the point b of Fig. 27 will follow the approximate path a-b which bends continually to the right. This bending tendency is evident in Fig. 29, which represents the intersections of x and z (or the point b of Fig. 27) for a number of frequencies.

Figure 28. Vector diagram for a receiver with diaphragm blocked.