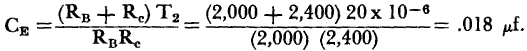| Transistor Basics is a free introductory textbook on transistors and their basic applications. See the editorial for more information.... |

|

Home  Transistor Oscillators Transistor Oscillators  Relaxation Oscillators Relaxation Oscillators  Basic Characteristics and Operation Basic Characteristics and Operation |
||






|
||
|
Basic Characteristics and OperationAuthor: Leonard Krugman One of the most inviting applications of the negative-resistance oscillator is as a relaxation type, particularly since its power requirements are low. Transistor relaxation oscillators have almost limitless use where a complex waveform, pulse generation, triggered output or frequency division is required. Like the equivalent vacuum-tube types, the periodic operation of the transistor relaxation oscillator usually depends on a R-C or R-L combination for the storage and release of signal energy. For this reason, they are characterized by abrupt changes from one operating point to another. This makes relaxation oscillators particularly useful for generating sawtooth waveforms.
Fig. 6-17. (A) Bask emitter-controlled relaxation oscillator with (B) idealized characteristic, and (C) waveforms. Figure 6-17 represents the basic emitter-controlled relaxation oscillator and its idealized current-voltage characteristic. The location of the frequency-determining network in the emitter circuit provides the largest measure of control. This basic type, therefore, is the most useful. The fundamental operation is involved, but not difficult to understand. For simplicity, assume the operation starts at point A (Figure 6-17B). At this point the transistor is cut off, since the emitter is biased in the reverse direction (-EA). Because of this reverse bias, the input circuit offers a high resistance path. The charge on capacitor CE (equals -EA) has to leak off through RE, and the rate of discharge is determined by the time constant RECE.
 almost instantaneously. In this instant, the operating point moves rapidly from point B through point C to point D. At the same time, the voltage across the capacitor starts to increase to its original value of -EA. The rate is fixed by the time constant of CE and the parallel equivalent of RB and Rc. In the meantime, the emitter current decreases at the same rate, thereby moving the operating point back toward point C. almost instantaneously. In this instant, the operating point moves rapidly from point B through point C to point D. At the same time, the voltage across the capacitor starts to increase to its original value of -EA. The rate is fixed by the time constant of CE and the parallel equivalent of RB and Rc. In the meantime, the emitter current decreases at the same rate, thereby moving the operating point back toward point C.
When the current reaches point C, operation passes from the saturation region to the negative-resistance region. Instability in this area causes the current to drop instantaneously to its value at point B. Because of this rapid drop, the condenser voltage does not change. The operating point returns to point A, and the condenser discharge action starts the cycle again. Note that there are two time constants during a complete cycle. The first one T1 = RECE controls the discharge rate of the condenser when operation moves from point A to point D. The second time constant
The frequency of the current wave is the same, but the waveform approximates a pulse, since the current only flows during the period when the condenser is charging (T2). This simple oscillator, then, is useful as a voltage sawtooth or a current pulse generator. The following problem will be used as a numerical example of basic relaxation oscillator design. Assume that a sawtooth voltage wave is required for use in a sweep circuit, and that the following characteristics are specified; frequency is 5 kc; the charging rate interval T2 is limited to 10% of the total cycle; RB is 2,000 ohms, required for sustained oscillation; Ec is fixed at 12 volts. The numerical values of the major operating points shown on Fig. 6-17 (B) are: for point A, IE = -0.1 ma, EE = 10 volts; for point B, IE = 0.01 ma, EE = 2 volts; for point C, IE = 3 ma, EE = 10 volts; and for point D, IE = 5 ma, EE = 2 volts. From the preceding analysis, Thus at point D,
The overall time constant To = T1 + T2 = Since
Since Ta = RECE,
|
||
Home  Transistor Oscillators Transistor Oscillators  Relaxation Oscillators Relaxation Oscillators  Basic Characteristics and Operation Basic Characteristics and Operation |
||
Last Update: 2010-11-17





 controls the charging rate when operation moves from point D to point A. The sawtooth voltage generated by this circuit is illustrated in Fig. 6-17 (C). The frequency of operation is approximately
controls the charging rate when operation moves from point D to point A. The sawtooth voltage generated by this circuit is illustrated in Fig. 6-17 (C). The frequency of operation is approximately .
.
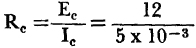 = 2,400 ohms
= 2,400 ohms = 200 μ seconds, T2 = 10% (To) = .10 (200) = 20 μ seconds, and T1 = To - T2 = 200 - 20 = 180 μ seconds.
= 200 μ seconds, T2 = 10% (To) = .10 (200) = 20 μ seconds, and T1 = To - T2 = 200 - 20 = 180 μ seconds. ,
,