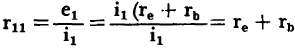Circuit Parameters

Author: Leonard Krugman

The general open-circuit characteristics derived for the grounded base connection apply equally well to the grounded emitter and grounded base connections, since the characteristics were determined on the basis of a sealed box. However, since the internal parameters of the transistor have been rearranged, the values of the general characteristics are different. It is necessary then, to evaluate the open-circuit characteristics r₁₁ r₁₂, r₂₁, and r₂₂ in terms of the transistor internal parameters r_e, r_b, r_c, and r_m. The same basic measuring circuits, illustrated in Figs. 3-8, may be used to determine the four-terminal parameter for the grounded emitter connection:

These grounded-emitter relationships are derived as follows:

A.

Using Fig. 4-1 (B), the input loop equation on the basis of Kirchoff's law is:

e₁ = i₁ (r_e + r_b) + i₂r_e

when

i₂ = 0, e₁ = i₁(r_e + r_b)

then

B.

For the same input loop equation, when i₁ = 0

e₁ = i₂r_e;

then

C. 

The output loop equation for Fig. 4-1 (B) on the basis of Kirchoff's law is:

e₂ - r_mi_c = i₁r_e + i₂ (r_e + r_c)

Also

i_e = -(i₁ + i₂)

Substituting for i_e,

e₂ + i_m (i₁ + i₂) = i₁r_e + i₂ (r_e + r_c) e₂ = i₁ (r_e - r_m) + i₂ (r_e + r_c - r_m)

when

i₂ = 0, e₂ = i₁(r_e-r_m)

then

D.

Using the same equations as in C above, when

i₁ = 0, e₂ = i₂ (r_e + r_c - r_m)

then

The open-circuit characteristics can now be numerically evaluated for the typical point-contact and junction transistors previously considered in Chapter 3. For the point-contact transistor in the grounded emitter connection:

r₁₁ = r_e + r_b = 150 + 100 = 250 ohms

r₁₂ = r_e = 150 ohms

r₂₁ = r_e- r_m = 150 - 23,900 = -23,750 ohms

r₂₂ = r_e + r_c - r_m = 150 + 11,900 - 23,900 = -11,850 ohms

For the junction transistor in the grounded emitter connection:

r₁₁ = r_e + r_b = 50 + 500 = 550 ohms

r₁₂ = r_e = 50 ohms

r₂₁ = r_e- r_m = 50 - 1,899,500 = -1,899,450 ohms

r₂₂ = r_e + r_c - r_m = 50 + 1,999,500 - 1,899,500 = 100,050

Because of the large values of r_m and r_c with respect to r_e, r₂₁ in the practical case can be approximated by -r_m, and r₂₂ by (r_c - r_m). The emitter resistance, r_e = r₁₂, is the feedback resistance and is equivalent to r_b = r₁₂ in the grounded base connection. Notice, however, that since there is phase inversion in the grounded emitter connection, r_e produces degenerative (negative) feedback, rather than regenerative (positive) feedback. The degenerative effect of the output current through r_e is similar to the degenerative action of an unbypassed cathode resistor in a grounded cathode vacuum tube.