You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
| You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.
|
| See also: cluster analysis |   |
In order to apply multivariate models successfully you need to have some knowledge about the structure of your data. Depending on the kind of analysis (classification or calibration) you should look for several aspects of the data set.
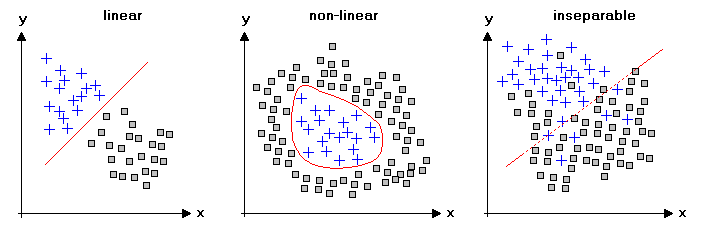
In the case of classification problems there are basically three cases to be distinguished: (1) data sets with linearly separable classes, (2) data with non-linearly separable classes, and (3) classes which cannot be separated at all. In all three cases the user should be aware that it is not a trivial task to decide which type of problem is addressed in the multi-dimensional case. Furthermore, the selection of the most suitable predictors strongly depends on these issues (see below). So, in general, one has to experiment and to 'play' with the data before setting up a classifier.
In the case of calibration problems there are two aspects which
should be considered prior to developing a calibration model of the data:
(1) Is a linear model sufficient to describe the relationship between predictors
and target variables, or (2) is it necessary to use a non-linear model
in order to set up a model. Again, this decision is easy, and is made even
more complicated by extensive noise in the data. In the case of noise,
a non-linear relationship may be hidden, so that it is impossible to create
a non-linear model.
Last Update: 2004-Jul-03