You are working with the text-only light edition of "H.Lohninger: Teach/Me Data Analysis, Springer-Verlag, Berlin-New York-Tokyo, 1999. ISBN 3-540-14743-8". Click here for further information.

Table of Contents Multivariate Data Modeling Classification and Discrimination Self Organizing Maps	Index
See also: ANN - Introduction

Kohonen Networks

The Kohonen network (or "self-organizing map" or SOM, for short) has been developed by Teuvo Kohonen. The basic idea behind the Kohonen network is to set up a structure of interconnected processing units ("neurons") which compete for the signal. While the structure of the map may be quite arbitrary, most implementations support only rectangular and linear maps.

The SOM defines a mapping from the input data space spanned by x₁..x_n onto a one- or two-dimensional array of nodes. The mapping is performed in such a way that the topological relationship in the n-dimensional input space is maintained when mapped to the SOM. In addition, the local density of data is also reflected by the map: areas of the input data space which are represented by more data are mapped onto a larger area of the SOM.

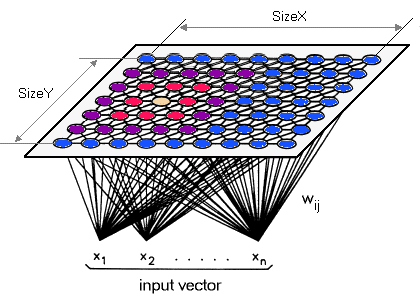
Each node of the map is defined by a vector w_ij which is adjusted during the training. The basic training algorithm is quite simple:
 

1) select an object from the training set
2) find the node which is closest to the selected data (i.e. the distance between w_ij and the training data is a minimum)
3) adjust the weight vectors of the closest node and the nodes around it in such a way that the wij move towards the training data
4) repeat from step 1) for a fixed number of repetitions

Kohonen maps may be arranged in any neighborhood relationship. A simple but interesting application is the usage of Kohonen maps to solve the travelling salesman problem. Start the  to see how it works. You can also go to the  to perform some further experiments with Kohonen networks.
 

Last Update: 2006-Jän-17