| Teach/Me Instrumentelle Analytik ist ein bei Springer, Heidelberg, erschienenes CDROM-basiertes Lehrbuch zur instrumentellen chemischen Analytik. Weitere Informationen finden sie hier.... |

|

Home  Massenspektrometrie Massenspektrometrie  Interpretation von Massenspektren Interpretation von Massenspektren  Metastabile Ionen Metastabile Ionen  Metastabile Ionen Metastabile Ionen |
||||||||||||||||||||||||||||||
| Siehe auch: Interpretation von Massenspektren | ||||||||||||||||||||||||||||||






|
||||||||||||||||||||||||||||||
Metastabile Ionen
Ein kleiner Anteil an Ionen wird jedoch während des Fluges im Massenspektrometer zerfallen. Passiert der Zerfall im Magnetfeld (oder bei doppelfokussierenden Geräten auch im elektrischen Feld), so werden die Bruchstücke auf die Gerätewand fliegen und entladen. Zerfällt das jeweilige Ion jedoch in einer der feldfreien Zonen (vor dem Magnet, bzw. zwischen Magnet und elektrostatischem Analysator bei doppelfokussierenden Geräten), so ergeben sich für die Bruchstücke stabile Flugbahnen. Damit werden diese Ionen detektiert, allerdings unter einer falschen Masse. Nehmen wir an, dass ein Ion A+mit der Masse ma und der Geschwindigkeit v aus der Ionenquelle austritt. Es besitzt damit die kinetische Energie von
Zerfällt nun das Ion A+ in das Ion B+ und das Neutralteilchen C, so treten die beiden Teilchen mit den Massen mb und mc mit der Geschwindigkeit v in das Magnetfeld ein. Das Neutralteilchen wird geradeaus fliegen und an die Wand prallen, während das geladene Teilen B+ durch das Magnetfeld abgelenkt wird. Die Geschwindigkeit des Teilchens A+ lässt sich wie oben berechnen:
woraus sich die Geschwindigkeit ausdrücken lässt:
setzt man Gleichung (2) in Gl. (4) ein und formt ein wenig um, so erhält man:
Führt man mit m* die Masse des metastabilen Teilchens ein, so erhält man dafür
Die scheinbare Masse des Fragments ist also geringer als die Masse mb. Die Breite des metastabilen Peaks rührt von der breiten Energieverteilung der metastabilen Teilchen her. Metastabile Peaks haben für die Interpretation eines Massenspektrums eine wichtige Bedeutung, da damit Massendifferenzen zugeordnet werden können. Ein metastabiler Peak ist immer der Beweis, dass das Ion m2 aus dem Ion m1 gebildet wird (in einem einstufigen Zerfallsprozess). Die Geschwindigkeitskonstante des Zerfallsprozesses liegt zwischen 104 und 106 s-1, was einem sehr schmalen Energieband entspricht. Das erklärt auch warum die Intensität der metastabilen Peaks generell klein ist.
|
||||||||||||||||||||||||||||||
Home  Massenspektrometrie Massenspektrometrie  Interpretation von Massenspektren Interpretation von Massenspektren  Metastabile Ionen Metastabile Ionen  Metastabile Ionen Metastabile Ionen |
||||||||||||||||||||||||||||||
Last Update: 2010-12-14


 (1)
(1) (2)
(2) (3)
(3)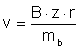 (4)
(4) (5)
(5) (3)
(3)